| The
force worked out on 07-05-2000, Protocosm force problem
solved on 02-09-2001
A real particle is a spatial wave falling down by itself
and standing up to the amplitude. It is oscillating. While
this, the radius R is moved between next to zero and to the
amplitude Ro. I call this particle a primary
quantum. There would be pure gravitational quanta and pure
electric quanta. Then we would explain gravitational particles
and electric charges. But charges really are coupled at
gravitational particles this way we find both kinds of
particle quanta in one system of symbiosis of nature. Now I
had the idea after all that the phenomenon of spatial
vibrating was the fundament of the exchange of momenta. During
this, the primary wave quanta would be exchanged between real
particles and charges. Wave quanta themselves aren't
particles. Therefore I don't speak of "virtual
particles" like present physics does. Particles
as real quanta and primary
oscillators are always just transmitters
and
receivers of spatial wave
quanta forming gravitation and electrostatics! Inside, there
is a returning spatial wave. Outside, a projection of it
generates the primary external wave. I
presented the following theses:
- If you enlarge the elongation R up to the amplitude Ro
virtually over Ro, then you get the particle as
transmitter of an external spatial
wave.
- The larger now the extension radius ri of the
spatial wave is, the smaller is the momentum mass mi
acting there, which was exactly measured with rest mass mo
or rest charge eo at the amplitude Ro.
- When two elementary masses exchange their momenta, the
force between both is arising while both distances ri
are multiplied now to ri².
- Each force between compact masses and charges is
combined of all elementary vectors of the exchange between
the elementary oscillators.
- For this behavior the rest mass mo and the
rest charge eo are valid as primary wave
quantum of the momentum exchange between oscillators.
- But also secondary wave quanta of magnet fields, mw
and ew, are acting this way, but not totally
spherical.
So I consequently followed: The center of gravity of a
compact external mass is just a virtual center, because it represents
the resulting force FR of all the interaction
forces Fi over their interaction radii ri
between microcosmic oscillators.
The gravitation force Fg = FR of this
compact mass is vectorially added from single forces Fi
at each particle interaction.
This way interacting momentum masses are streaming from all
directions of the universe to all the given masses. The
general inertia is shown now as if a medium would
"stream" to the earth but in the same amount off of
the earth, too. In every inertia equilibrium the momentum
masses should be the same into all directions.
Then I made the equations:
as conservation of angular momentum Jo
follows:
from which follows:
|
mi = mo Ro / ri
(hyperbolic) |
(3) |
|
xo = mi ri = mo
Ro torque xo in conservation |
(4) |
or
or the terms of momenta:
|
pi = po Ro / ri
= mi c = mo c Ro / ri |
(5) |
At the position of interaction with the
other quantum (mass or elementary charge) only the momentum
mass mi is effectively working which was at the
amplitude after equ. (7):
|
Fg = G mo mo / ri² |
(6) |
|
Fg = G mi mi / Ro² |
(7) |
|
Fg = Fa = mo a |
(8) |
|
Fo = Mo ao with ao
= - G Mo / Ro² |
(9) |
|
Fo = - G Mo Mo / Ro² |
(10) |
Mo is the internal mass of a
quantum at the surface Ro. Both are acting after
the coupling constant a3.
Additionally my theory found the relations:
|
Fo = - c4 / G |
(11) |
|
Mo = h c / G mo |
(12) |
|
Fo = - h² c² / G mo²
Ro² |
(13) |
|
Fo = - h² c² / G mo
Ro mi ri |
(14) |
|
|
xo = mo Ro |
xo = mi ri |
Analysis: G = - c4 / Fo
|
Fg = mo mo c4
/ ri² Fo ~ F² / Fo |
(15) |
Therefore mc²/r multiplied with mc²/r is
already F² or
|
F1 F2 / Fo |
|
|
|
(16) |
|
Fg = |
moc² |
moc² / Fo |
|
(17) |
|
|
ri |
ri |
|
|
|
Fg = |
E1 |
E2 / Fo |
E = FA ri |
|
|
|
ri |
ri |
|
|
|
Fg = |
FA1 |
FA2 / Fo |
standard equ. of forces |
(18) |
Each mass has its own force FAn,
which has the relationship with elementary force!
With equ. (5) we get:
|
Fg = mi1
c² mi2 c² / Fo Ro² |
Eo = Fo Ro |
(19) |
|
|
Mo = Eo /c² |
|
|
Fg = mi1 c mi2 c / Mo
Ro |
pi = mi c |
(20) |
|
Fg = pi1 pi2 / Mo
Ro with the torque |
Do = Mo Ro |
(21) |
The gravitation force Fg after
Newton is the result of two momenta pi at the
radius ri acting with the momentum mass mi,
referred to the constants of the quantum, the particle or the
elementary charge as oscillator like Fo, Ro
or Mo.
THIS IS THE SIMPLE PROOF OF AN EXCHANGE FORCE AFTER MY
UNITED FIELD THEORY!
But it obviously has no importance for calculations of
forces. It only shows like force is made.
What is valid for gravitation force must be valid for
electric charge following my theory, because the elementary
charge represents an elementary quantum spatially vibrating in
the same way like a particle mass and transmitting a spherical
wave into the exchange space. I calculate:
|
mo = eo kq |
(22) |
|
Fg = ei1 c ei2 c kq²
/ Moq Roq |
(23) |
|
pi = ei c kq |
(24) |
Just here the local momenta are exchanged.
How are the relations at secondary wave quanta?
If a mass or a charge would rotate elementary, then they
would form secondary momenta with the secondary velocity v and
the secondary rotation radius Rrot. We get the
secondary quanta, which exchange their momentum masses into
the space, too, but now not as spherical wave but as a spatial
wave of two directions (two maxima) of the acting dipole what
is a magnet field. We get the first twist of geodetic lines of
the primary wave quanta by this first kind of rotation. If the
plane of rotation is rotating once more around itself, then
the dipole directions change at the receiver. We get a
frequency of the secondary exchange wave. This second twist
leads to the x-frequent exchange wave. Also here the
conservation of angular momentum is valid:
|
J(n) = nh = mw(n)
c Rw(n) = mo v Rw(n) / g
= gmo v Rrot(n) |
(w1) |
|
mw(n) = f (n), f(R w(n)), f(mo),
f(v), f(g) |
|
|
g = (1 – v² / c²)1/2 |
|
|
(Gamma factor of special relativity theory) |
|
|
mA = mo / g |
|
|
indicated mass, retardation mass, observer indicated
the impacting mass |
|
|
mB = g mo
with pB(n) = mB(n) v = mb(n)
c |
|
|
Mass in movement, observer is flying along the moving
mass |
|
|
mw(n) = mo v / c g |
(w2) |
The local secondary wave momentum exchange
is then:
|
J(n) = nh = mi(n)
c ri(n) |
(w3) |
|
pi(n) = pw(n) Rw(n)
/ ri(n) |
(w4) |
|
pw(n) = mw(n) c |
(w5) |
|
pi(n) = mi(n) c |
(w6) |
Analogously (3) is valid:
|
mi(n) = mw(n) Rw(n)
/ ri(n) |
(w7) |
and the secondary dipole forces are
analogously (6) and (7):
|
Fgw = G mw(n) mw(n)
/ ri(n)² |
(w8) |
|
Fgw = G mi(n) mi(n)
/ Rw(n)² |
(w9) |
Now one can form the forces (w8) and (w9)
over the wave mass mb(n), too. Then we get the
analogon on the action of rest masses and/or rest charges.
Therefore I didn't derive them completely:
|
FgB = G mb(n) mb(n)
/ ri(n)² |
(w8a) |
|
FgB = G mi(n) mi(n)
/ Rrot(n)² |
(w9b) |
Here it's possible now to underrun the wave
amplitude Rw(n) with the distance ri(n)
going to the center of the rotating mass (or to the rotating
charge).
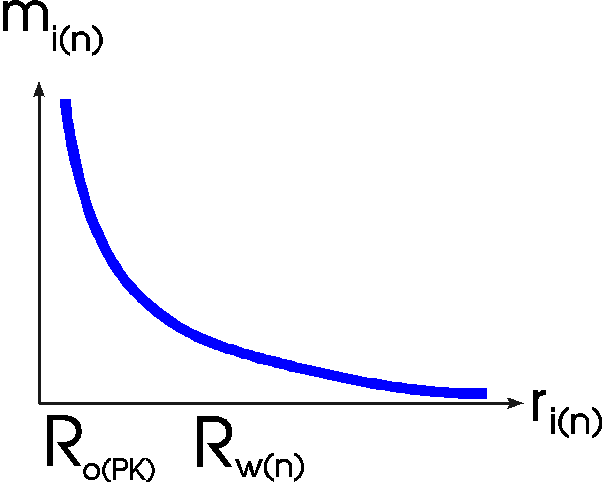
The force Fgw would go to infinite singularly if
the distance would reach zero.
But what is a distance here? If there is something, the
distance never can reach zero! But what is there? The answer
our theory gives to us: if there is no stable quantum like a
particle acting with its amplitude, so there must be a protocosm
- the early stage of a quantum in unstable or better in
divergently open form. Because in this feature of protocosms
is no mass which would have made it for divergent contracting
but only field energy, we call it field
protocosm. It realizes a divergent field force Fo(PK)
next to Fo and also an intrinsic internal amplitude
of Ro(PK).
This way a rotating field, the so-called magnetic field
is a complete analogon to the primary field of masses and
charges, no matter if it's caused gravitationally or
electrically. You see that the attraction between magnets
aims to the center laying inside of the causing orbit, no
matter how and on what orbit they are ever made during the
rotation of masses or charges. While this, the force and
the spacetime curvatures increase to finite maxima. These
protocosms are strongly larger at superconductors.
Now an equation should be found which describes the central
protocosm.. At first I take the well-known equation of the
gravitational horizon ro:
The external radius of the protocosm ro
is dependent on the internal mass Mo.
Now we could substitute the momentum mass mi(n)
in the distance ri(n) of the center of rotation
from equ. (w7) instead of the internal mass Mo,
just as it would make the protocosm (PK) from wave functions:
|
ro(PK) = 2 G mw(n) R w(n)
/ ri(n) c² |
(w11) |
Here we see: If the velocity is increasing
the relativistic momentum mass mw(n) is also
increasing, while the wave amplitude Rw(n) is
decreasing. Therefore the horizon ro(PK) is only
still dependent on the distance ri(n). When the
distance decreases, a value can be reached which is finally
the same as the horizon. This statement doesn't help us going
on.
Now we substitute the internal mass Mo directly
by the wave masse mw(n), this equation follows:
|
ro(PK) = 2 G mw(n) / c² = 2 G
mo v / g c³ |
(w12) |
Here the horizon ro(PK) is a
function of the decelerated mass mo, of the
velocity v and of the gamma factor g
of the special relativity theory.
You see: the horizon grows along the increasing mass, but
essentially it grows along the velocity which is changed or
totally stopped by movement of this mass. The g.m. protocosm
is then dependent on the special-relativistic conditions of
the velocity changes (the same is valid for electric charges
and their e.m. protocosms)!
This kind of protocosms can only be build if an INTERACTION
was just running.
If there aren't an interaction then the mass mo
rotates as movement mass mB(n) on its orbit (see
equ.(w1)).
We can make the movement momentum mass mb(n)
from it:
Now we set it into the horizon and get this:
|
ro(PK) = 2 G mb(n) / c² = 2 G
mo v g / c³ |
(w14) |
Just now the gamma factor acts as soon as
relativistic velocities appear working against the increase of
the horizon with given mass and increasing velocity. From this
I see the parallel to the general relativity theory. Here the
adjustment of a gravitational horizon is only dependent on the
intensity of the resting mass (see equ. (w10)).
So we conclude:
- The protocosm from wave masses mw(n) is made
from interactions especially from relativistic velocity
changes.
- This protocosm of the moved masses mb(n) is
made from the intensity of the masses or/and of the
charges which are non-relativistically moved.
For superconductors is then valid:
- for b): If there a current is flowing, it makes a
non-relativistic protocosm from intensity. Since present
currents are too low, the shielding effect of that
protocosm is also too low.
- for a): If the superconductor additionally rotates, you
can support a relativistic interaction by strong
deceleration which forms a bigger protocosm having a
stronger shielding similar with Podletnikov's effect with
about 2%.
Who will come along? Who wants to build a stronger
superconductor with more initial intensity? Who wants to
increase the rotation velocity and its retardation
relativistically?
Who makes this, who will produce a protocosm of real
effectiveness.
Conclusio:
But if we found a description of the central protocosm,
then we had the proof for strong space curvatures in each
force centers. The more we could amplify them, the more
curvatures we would get into larger areas of our space. This
would allow us to change physical magnitudes after Einstein's
relativity. I saw here the action of the superconductivity
which doesn't only "shield" the gravitation how
Podletnikov and different scientists suspected, but which
curves the spacetime effectively. Just now, exactly between
two points the synthetic space curvature is acting, no matter
what distance they ever have (influence of the other forces
and curvatures neglected first). It shifts the action of
gravitation, of electromagnetism, and it shifts the time. At
2%, a clock already should be slow by 29 minutes per day next
to the superconductor.
From my acknowledge I see my copyright to be the originator
and the discoverer of the protocosms, even of the synthetic
protocosms, which qualities we can examine and use later. How
these properties look like I will tell you another time
another place.
My site: https://www.arcusuniverse.com
|
